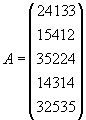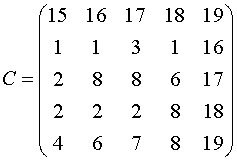Решение задачи о назначениях
Еще одна из выделенных задач линейного программирования, о которой важно упомянуть — это задача о назначениях. Вообще говоря, можно считать, что это частный случай транспортной задачи, для которой мощности поставщиков и потребности клиентов равны 1 (и обычно совпадает размерность). Если на примерах, это может быть задача назначения работников на должности (с достижением максимальной эффективности, или, может, минимальных затрат на зарплату), назначение машин на производственные линии и т.п., при этом один исполнитель (человек, машина, орудие и т.п.) может выполнять только одну работу.
Так же как для решения транспортной задачи был модифицирован симплекс-метод и разработан метод потенциалов, так и для задачи о назначениях был создан более подходящий (более краткий) метод решения. Чаще всего используется так называемый венгерский метод (см. решение примера 1 ниже).
Ниже выложены примеры задач о назначениях, решенные разными способами — изучайте, ищите похожие, решайте. Если вам нужна помощь в выполнении заданий, перейдите в раздел: Решение задач линейного программирования для студентов.
Задача о назначениях: примеры решений онлайн
Задача 1. Решить задачу об оптимальном назначении с матрицей эффективностей A.
Задача 2. Решить задачу о назначениях.
Задача 3. Четыре работника должны выполнять четыре вида работ. Назначить работников на работы методами динамического программирования и ветвей и границ таким образом, чтобы затраты труда были минимальны.
Источник
Задача о назначениях
Типичное задание:
В цехе предприятия имеются 5 универсальных станков, которые могут выполнять 4 вида работ. Каждую работу единовременно может выполнять только один станок, и каждый станок можно загружать только одной работой.
В таблице даны затраты времени при выполнении станком определённой работы. Определить наиболее рациональное распределение работ между станками, минимизирующее суммарные затраты времени.
Задача. Служба занятости имеет в наличии четыре вакантных места по разным специальностям, на которые претендуют шесть человек. Проведено тестирование претендентов, результаты которого в виде баллов представлены в матрице
Распределить претендентов на вакантные места таким образом, чтобы на каждое место был назначен человек с наибольшим набранным по тестированию баллом.
Пример решения задачи о назначении с минимальной стоимостью;
Пример решения задачи о назначении с максимальной стоимостью;
Постановка задачи о назначениях
В таблице 1 приводятся оценки возможных транспортных издержек.
Таблица 1 — Оценки транспортных издержек
R j Q i | 25 | 32 | 5 | 4 |
30 | 5 | М | 25 | 26 |
35 | 10 | 3 | 30 | 31 |
5 | М | М | 0 | 1 |
5 | М | М | 0 | 1 |
Переменные. В качестве переменной введем величину
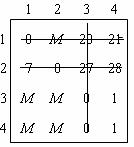
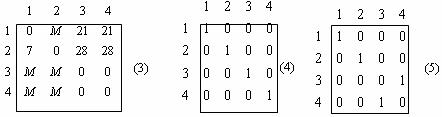
Все предполагаемые алгоритмы поиска решения задачи о назначениях базируются на следующем утверждении: оптимальное решение задачи не изменится, если к любой строке или столбцу матрицы издержек прибавить (или вычесть) постоянную величину в силу того, что приоритет назначения не изменится. И весь алгоритм ведется на матрице издержек с соответствующими преобразованиями для получения в ней нулевых элементов, образующих систему так называемых «независимых нулей». Число независимых нулей равно размерности матрицы, а их расположение таково, что каждый из них встречается один раз в строке и один раз в столбце. Если такие независимые нули будут найдены, то в матрице решения в соответствии с их положением будут проставлены единицы. В матрице 1 нулевые элементы получены вычитанием наименьшего элемента в каждой строке. (1)
Как только будут получены нулевые элементы, применяют различные алгоритмы: Мака, венгерский, минимальных линий. Рассмотрим процедуру вычеркивания нулевых элементов минимальным числом прямых линий. В матрице 2 показано, как используется это правило. Могут быть и другие варианты вычеркивания. 
Если все нулевые элементы в матрице будут вычеркнуты, а минимальное число линий будет равно размерности матрицы, то независимые нули в матрице существуют, и решение найдено. В противном случае выбирается наименьший элемент из невычеркнутых элементов (он равен 1). Этот элемент вычитается из каждого невычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.
В результате получается матрица (3), которая указывает на два оптимальных решения (матрицы решений 4 и 5).
Следует заметить, что, если на последнем шаге оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение.
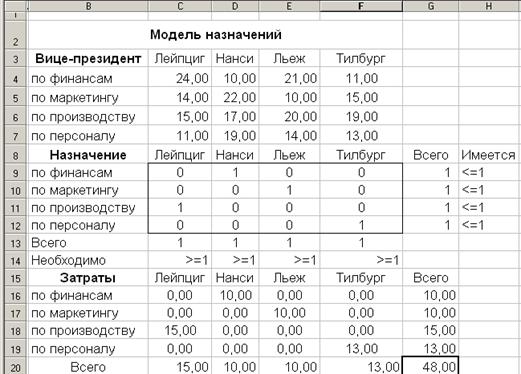
Модель назначений
Пример . Руководство фирмы приняло решение произвести инспекцию своих предприятий в Лейпциге, Нанси, Льеже и Тилбурге, направляя туда своих вице-президентов, каждый из которых в компании возглавляет одно из направлений (финансы, маркетинг, производство и персонал). Хотя может существовать большое число факторов, которые нужно учесть при таком назначении (знание языка, узкая специализация, невозможность оторваться от прямых обязанностей и т. д.), руководство компании решило оптимизировать в качестве первого шага только суммарные затраты на командировку вице-президентов. Таблица командировочных расходов в различные города (тыс. долларов) приведена ниже.
| Вице-президенты | Лейпциг | Нанси | Льеж | Тилбург |
| По финансам | 24 | 10 | 21 | 11 |
| По маркетингу | 14 | 22 | 10 | 15 |
| По производству | 15 | 17 | 20 | 19 |
| По персоналу | 11 | 19 | 14 |
Требуется составить схему распределения вице-президентов по филиалам, минимизирующую командировочные расходы.
Решение. Табличная модель этой задачи после проведенной оптимизации приведена на рис.
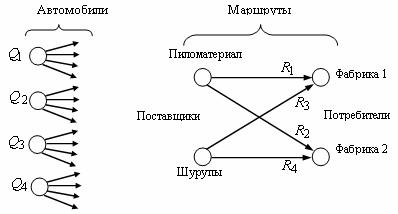
Модель назначений является разновидностью транспортной модели. От последней она отличается только тем, что в ней единица предложения не может распределяться по нескольким местам назначения (ср. рис.).
Таким образом, модель назначений всегда можно построить в виде транспортной модели, в которой предложение в каждой исходной точке и спрос в каждом конечном пункте равны единице.
Точно так же, как и транспортная модель, модель назначений может быть несбалансированной, содержать недопустимые назначения, иметь альтернативные решения при одном и том же значении целевой функции. Эти варианты моделей назначения строятся в полной аналогии с соответствующими транспортными моделями.
Оптимальное распределение продавцов по торговым точкам
Задание. Существует 4 продавца А1, А2, А3, А4 и 4 торговые точки В1, В2, В3, В4. Эффективность работы продавцов на торговых точках задаётся следующей матрицей:
| 9 | 3 | 4 | 8 |
| 4 | 6 | 7 | 11 |
| 5 | 8 | 8 | 4 |
| 6 | 12 | 15 | 9 |
Найти оптимальное распределение продавцов по торговым точкам.
Поскольку задана матрица эффективности, то искать необходимо максимальные значения, следовательно, целевая функция стремится к максимуму. Именно поэтому при решении выбираем вид Максимальная прибыль .
Модифицируем матрицу умножением всех элементов на (-1) и затем сложением их с максимальным элементом матрицы (15) так, чтобы матрица не содержала бы отрицательных элементов:
| 6 | 12 | 11 | 7 |
| 11 | 9 | 8 | 4 |
| 10 | 7 | 7 | 11 |
| 9 | 3 | 0 | 6 |
Шаг №1.
1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
| 0 | 6 | 5 | 1 | 6 |
| 7 | 5 | 4 | 0 | 4 |
| 3 | 0 | 0 | 4 | 7 |
| 9 | 3 | 0 | 6 | 0 |
Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент:
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
| 0 | 0 | 0 | 0 |
После вычитания минимальных элементов получаем полностью редуцированную матрицу.
2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
Фиксируем нулевое значение в клетке (1, 1). Другие нули в строке 1 и столбце 1 вычеркиваем.
Фиксируем нулевое значение в клетке (2, 4). Другие нули в строке 2 и столбце 4 вычеркиваем.
Фиксируем нулевое значение в клетке (3, 2). Другие нули в строке 3 и столбце 2 вычеркиваем.
Фиксируем нулевое значение в клетке (4, 3). Другие нули в строке 4 и столбце 3 вычеркиваем.
В итоге получаем следующую матрицу:
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
Количество найденных нулей равно k = 4. В результате получаем эквивалентную матрицу Сэ:
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
4. Методом проб и ошибок определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить максимальное значение прибыли.
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
Cmax = 9 + 11 + 8 + 15 = 43
Таким образом, распределение продавцов по торговым точкам будет следующее:
1 продавец – торговая точка №1
2 продавец – торговая точка №4
3 продавец – торговая точка №2
4 продавец – торговая точка №3.
При таком назначении, максимальная эффективность составит 43.
Источник
Задача о назначениях онлайн
С помощю этого онлайн калькулятора можно решить задачу о назначениях (задачу о выборе) венгерским методом. Для решения задачи о назначениях задайте размерность матрицы, выберите из вариантов «максимальная прибыль» и «минимальные расходы». Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Предупреждение
Задача о назначениях − теория
Математическая задача о назначениях или задача о выборе формулируется следующим образом. Требуется выбрать такую последовательность элементов 
из следующей квадратной матрицы
 |
чтобы 
достигала своего максимального значения, причем 
при 
. Другими словами, нужно выбрать из каждого столбца и каждой строки ровно по одному элементу так, чтобы их сумма была максимальной.
Отметим, что если бы матрица C была устоена так, что максимальные элементы каждой строки лежали бы в разных столбцах, то решение задачи было бы элементарным, т.е. к качестве решения нужно было выбрать эти максимальные элементы. Однако обычно максимальные элементы нескольких строк(столбцов) расположены в одном и том же столбце (строке) и решение проблемы затрудняется.
При решении задачи о назначениях применяется венгерский метод, что существенно упрощает решение задачи.
Венгерский метод
Сделаем несколько определений.
1. Нулевые элементы 
квадратной матрицы S будем называть независимыми нулями , если столбец и строка, в которых находится данный нулевой элемент не содержат другого нулевого элемента.
2. Две прямоугольные матрицы 
и 
порядка mxn называются эквивалентными, если 
, 
, 
.
Решение задачи имеет подголовительную и итерационную части.
Подготовительная часть. Для каждого столбца матрицы C найдем максимальный элемент и из этого элемента вычитаем каждый элемент данного столбца. (Если рассматривается задача на минимум, то находим минимальный элемент каждого столбца и из элементов данного столбца вычитаем этот минимальный элемент. Далее все по нижеизложенному алгоритму). В результате получим матрицу, в каждом столбце которой имеется нулевой элемент . Далее находим минимальный элемент каждой строки и из элементов данной строки вычитаем этот минимальный элемент. В результате получим матрицу, в каждой строке и в каждом столбце имеется по крайней мере один нулевой элемент.
Далее отмечаем звездочкой произвольный нуль в пероом столбце и просматриваем второй столбей и если в нем есть нули и в этой строке нет отмеченного нуля, то отмечаем данный нуль звездочкой. Аналогичным образом поступаем и с остальными столбцами. Отмеченные нули являются независимыми.
Этап 1. Если количество независимых нулей равно размерности матрицы, то задача решена и позиции отмеченных нулей является решением задачи о назначениях. Если же количество независимых нулей меньше n, то продолжаем процедуру. Выделяем столбцы матрицы C содержащие нули со звездочкой. Если среди невыделенных элементов матрицы нет нулевых, то переходим к этапу 3. Если обнаруживается невыделенный нуль, то есть два варианта:
Вариант 1. Строка, содержащая невыделенный нуль содержит также нуль со звездой. В этом случае ставим над найденным нулем знак °, выделяем строку, содержащую этот нуль, снимаем выделение из столбца, на пересечении которой с только что выделенной строкой находится нуль со звездой. Далее, если обнаруживается невыделенный нуль, переходим к этапу 1. Если невыделенных нулей нет, то переходим к этапу 3.
Вариант 2. Строка, содержащая невыделенный нуль не содержит нуль со звездой. В этом случае отмечаем этот нуль знаком ° и переходим к этапу 2.
Этап 2. Исходя из нуля со знаком °, в строке которой нет нуля со звездой (вариант 2) строим следующую цепочку элементов матрицы C: Исходный 0° − 0* (лежащий в одном столбце (если существует)) − 0° (лежащей в одной строке с предшествующим 0* и т.д. Цепочка имеет вид 0°−0*−0°−. и обязательно заканчивается 0°. Там, где 0°, заменяем на 0*, а на четных позициях уничтожаем знак * над нулями. Далее уничтожаем все ° над нулями и снимаем выделения из столбцов и строк. Число независимых нулей увеличился на единицу. Переходим к этапу 1.
Этап 3. К этому этапу переходим после завершения этапа 1, когда независимых нулей нет.
Среди невыделенных элементов находим минимальный q>0. Далее величину q вычитаем из всех элементов матрицы C расположенных на невыделенных строках, и прибавляем ко всем элементам на выделенных столбцах (можно и так: величину q вычитаем из всех невыделенных элементов матрицы C и прибавляем ко всем элементам, находящимся на пересечении выделенных строк и столбцов). В полученной матрице появятся невыделенные нули поэтому переходим к этапу 1.
Для рассмотрения численного примера задачи о назначениях (задачи выбора), введите в кальнуляторе в начале страницы элементы матрицы и нажмите на кнопу вычислить. Онлайн калькулятор выдаст подробное рашение задачи.
Источник