Понять Эйнштейна. Глава 4. Эффект Доплера
Глава 4. Классический эффект Доплера
В большинстве книг, посвященных специальной теории относительности, упоминается эффект Доплера. Без обсуждения эффекта Доплера, в самом деле, трудно обойтись, хотя для вывода основных положений СТО он нам не понадобится. Но с ним обязательно нужно разобраться, чтобы ответить в дальнейшем на очень популярный вопрос: «Как же будет выглядеть мир глазами человека, летящего в нем со скоростью, близкой к скорости света?».
Вообще, при изучении теории относительности, есть два неизбежных вопроса, которые и я себе не раз задавал: первый – это «Как выглядят все физические процессы, происходящие в одной СО, глазами наблюдателя другой СО, движущейся с большой скоростью относительно первой»; а второй, самый любимый, — «Как же, с какой скоростью, черт возьми, процессы происходят НА САМОМ ДЕЛЕ. ».
Ответы на них, как вы, наверно, уже догадываетесь, в релятивистской физике будут не просты. На второй вопрос, заранее признаюсь, вообще будет невозможно ответить однозначно, так как каждый наблюдатель С РАВНЫМ ПРАВОМ будет придерживаться своей шкалы расстояний, своего отсчета времени, и иногда даже разной временной последовательности для причинно-несвязанных событий. Причинно-связанные события, разумеется, сохранят свою последовательность, из какой бы системы отсчёта их ни наблюдали. Но об этом позже.
А сейчас я вас, возможно, удивлю: — Думаете, в классической физике ответ на оба вопроса прост и одинаков? То есть, для быстро движущегося наблюдателя происходящие события будут выглядеть так же, как для неподвижного – а именно так, как они и происходят НА САМОМ ДЕЛЕ? Ошибаетесь, друзья! Тут то впервые и появляется перед нами эффект Доплера. Эффект этот, на первый взгляд, не слишком сложен, и заключается в следующем:
Если имеются некий источник периодически повторяющихся сигналов (звуковых, электромагнитных) и наблюдатель, принимающий эти сигналы, то движение наблюдателя относительно источника приводит к изменению частоты принимаемых сигналов: если источник и наблюдатель сближаются – частота принимаемых сигналов возрастает, если они удаляются друг от друга – частота падает.
Чем ниже скорость распространения сигнала, тем меньшая скорость наблюдателя относительно источника нужна, чтобы заметить эффект Доплера. А потому понятно, что эффект Доплера раньше всего обнаружился для звуковых сигналов. Если быстро приближающийся к вам поезд или автомобиль даст продолжительный гудок, то вначале вы услышите звук высокий и пронзительный, а затем, когда гудящий транспорт поравняется с вами и начнет удаляться, звук резко изменится, станет низким и басовитым. Это и есть звуковой эффект Доплера.
Обычно в качестве периодичного сигнала рассматривают синусоидальную волну определенной частоты. Тогда эффект можно выразить несложными формулами, связывающими частоту или угловую скорость, длину волны, и скорость наблюдателя. Однако это совершенно необязательно. (Вы любите формулы, читатель? Я, если честно, — не очень!) Если уж мы говорим о звуках, то подходящим периодическим сигналом может быть и отрывистый писк таймера, и бой курантов, и барабанная дробь, и кваканье лягушки.
Попробуем привести наглядное объяснение эффекта Доплера без всяких формул. Будем, для примера, слушать бой часов на городской башне с некоторого расстояния (см. первые два рисунка в начале главы). Представьте себе, что только что часы показали 10:00 утра и пробили 10 ударов, а интервал между ударами составляет ровно 1 секунду. Представьте, к тому же, что вы слушаете бой часов на таком расстоянии, что звуку от башни требуется точно 10 секунд, чтобы достичь ваших ушей. Рисунок 1 соответствует в точности тому моменту, когда колокол в часах пробил последний раз, а звук первого удара как раз долетел до стоящего наблюдателя (это вы и есть). Рисунок 2 показывает ситуацию через 5 секунд после последнего удара часов – стоящий наблюдатель успел послушать 5 ударов, и ему предстоит услышать еще пять.
Теперь добавим к нашей картине еще одного наблюдателя. Пусть им будет летчик самолета, который как раз в момент, изображенный на первом рисунке, пролетал точно над вашей головой. А летел он в направлении на башню, и со скоростью очень близкой к скорости звука. Ясно, что первый удар часов он слышал одновременно с вами. А теперь взглянем на рисунок 2, который является ключевым для объяснения. По прошествии 5 секунд летчик пролетит почти половину пути до башни. И, в то время как стоящий наблюдатель будет слышать пятый удар часов, летчик будет слышать уже последний 10-й удар. Причем, совершенно очевидно, что до этого он успел прослушать все предыдущие девять.
Что из этого следует, вы наверно уже догадались сами. Летящий наблюдатель услышал 10 ударов за пять секунд, т.е. часы для него били чаще и отзвонили в два раза быстрее, чем для наземных наблюдателей. Если бы на площади перед башней играл на скрипке музыкант, то летчик слышал бы любую мелодию в два раза быстрее и в другой тональности, на октаву выше.
А вот если бы самолет летел в противоположную сторону, то звук с трудом догонял бы его, и тогда все звуки летчик бы слышал, наоборот, замедленными, с растянутыми промежутками и в пониженной тональности. Как видите, мы незаметно, но совершенно логично, расширили действие эффекта Доплера с регулярно повторяющихся сигналов на все звуки вообще.
Точно такой же эффект, какой возникает для звуковых сигналов, должен возникать и для световых. Световым сигналом, в широком смысле, является любое визуальное изображение, воспринимаемое глазом или прибором, а источником такого сигнала может быть любой освещенный (либо светящийся) объект, в том числе, все те же башенные часы. Я намерен показать, что эффект, который мы наблюдали со звуковым восприятием часов, будет происходить и с визуальным. Но, чтобы заметить его, потребуется много большая скорость движения наблюдателя относительно часов, ибо световой сигнал несравнимо быстрее звука: не 300 м/с, а 300.000 км/с
Для наглядной иллюстрации светового эффекта Доплера давайте нарисуем пару картинок, очень похожую на предыдущую. Мы только изменим масштабы расстояний, для чего поместим неподвижного наблюдателя на другую планету (например, Луну), самолет с летчиком заменим на ракету с космонавтом, летящую почти со скоростью света, а башню и циферблат часов вообразим такими большими, что их можно разглядеть с Луны. Кроме того, мы добавим на часах секундную стрелку, и вместо последовательности из 10 звуковых ударов используем последовательность изображений циферблата часов, отличающихся положением секундной стрелки. Понятно, что, если звон часов распространялся со скоростью звука, то визуальное изображение самих часов будет распространяться со световой скоростью (изображение, конечно, фокусируется уже в нашем глазу, но сути это совершенно не меняет).
Пусть, как и в прошлый раз, часы показывают примерно 10:00 утра. Положение стрелок на циферблате, которое (на рис.3) одновременно наблюдают лунный наблюдатель и космонавт в ракете, пролетающий рядом, говорит о том, что осталось 10 секунд до 10-ти часов – секундная стрелка, показанная красным цветом, смотрит на цифру «10», и ей остается сделать десять скачков до цифры «12», прежде чем часы покажут ровно 10:00.
От момента, изображенного на рис.3, до момента, изображенного на рис.4, с точки зрения лунного наблюдателя, прошло 5 секунд. Поэтому он на втором рисунке видит секундную стрелку, показывающую на цифру 11. А вот космонавт, летящий навстречу часам со скоростью, близкой к световой, успел увидеть за это время 9 скачков секундной стрелки. С его точки зрения, уже в следующее мгновение на часах будет ровно 10:00.
И то, что происходит с циферблатом часов, относится ко всему, что космонавт видит на Земле: для него быстрее происходят все земные события, все передвижения землян кажутся ему ускоренными в два раза. И значит, время на Земле, по наблюдениям космонавта, течет в 2 раза быстрее. Это кажущееся ускорение всех визуально наблюдаемых явлений и представляет собой эффект Доплера для света в классическом понимании.
Все выглядит вполне логично, не правда ли? Тем не менее, я ясно представляю, как читатель, уже знакомый с теорией относительности, в этом месте моего повествования недоуменно пожмет плечами и даже заподозрит меня в жульничестве. И не без оснований: ведь картинки, использованные нами для объяснения эффекта Доплера, нарисованы с точки зрения наблюдателя, неподвижного относительно Земли и часов. Для движущегося же наблюдателя, как нам предстоит убедиться в скором времени, картина происходящего выглядит несколько по-иному. Если для самолета, летящего со скоростью звука, эти изменения крайне незначительны и ими можно с легкостью пренебречь, то для такой быстрой ракеты, как в нашем втором примере, изменения расстояний и времени будут настолько велики, что не заметить их будет уже невозможно. А ведь регистрирует эффект Доплера, по определению, именно движущийся относительно часов наблюдатель — тот, что сидит в ракете. И если так, то правомерна ли вообще наша попытка объяснять оптический эффект Доплера в рамках классических представлений?
Но зададимся встречным вопросом: а в каких же еще рамках нам его рассматривать, если мы пока не знакомы с теорией относительности? И как иначе должны были понимать сдвиг частоты излучения, идущего с далеких космических объектов, физики и астрономы, столкнувшиеся с этим явлением задолго до появления работ Эйнштейна? Они объясняли его примерно также, как мы в наших рисунках. И сами рисунки не содержат никакой ошибки – они точно и правдиво отражают происходящее. Только, с точки зрения классической физики, эти рисунки содержат полную, исчерпывающую информацию о наблюдаемом явлении, а с позиций релятивистской физики, рисунки абсолютно верны, но содержат не полную, а частичную правду, отражая взгляд земного и лунного наблюдателей, но не космонавта. (Известная житейская поговорка, что «неполная правда хуже вранья», в этом случае вряд ли справедлива.) Для получения полной и объективной картины, в свете теории относительности, мы должны лишь дополнить имеющиеся рисунки другой серией рисунков – сделанной летящим в ракете космонавтом. Но то, что увидит космонавт, согласно СТО, мы пока изобразить не умеем.
Я намеренно стремился избежать математических формул и точных расчетов при первом знакомстве с эффектом Доплера. Если мы выразим визуальный эффект Доплера математическими формулами, выведенными по правилам классической физики, то эти формулы окажутся впоследствии неверными для света. Но – самое главное – они отразят беспомощность классической физики определить по величине Доплер-эффекта относительную скорость часов. Знаете, почему? Потому что кое-что ОЧЕНЬ ВАЖНОЕ ускользнуло от нашего внимания: дело в том, что для вычисления по классическим формулам требуется знать, в какой СО покоится СРЕДА, проводящая сигнал. Или, другими словами, с какой скоростью источник сигнала и наблюдатель движутся относительно среды распространения сигнала. В случае звукового сигнала, эта среда – воздух. И, если на первых двух рисунках дует сильный ветер (попутный либо встречный), то ветер непосредственно влияет на степень нарастания частоты сигнала для летчика (при встречном частота нарастает несколько медленнее, при попутном – быстрее; кому интересно, проверьте сами по классическим формулам). А вот в случае со световым изображением, эта среда – тот самый гипотетический «эфир», на поиски которого ушли (и до сих пор не вернулись) многие принципиальные противники СТО. А в СТО никакой «эфир» не понадобится. Там пустота она и есть пустота (и это огромное и бесспорное преимущество).
Рисунки, однако, отражающие суть эффекта Доплера, останутся пригодными и полезными в рамках нового релятивистского подхода.
Я снова забегу вперед и скажу следующее: эффект Доплера в релятивистской физике будет учитывать разный счет времени в СО наблюдателя и источника, который нам еще предстоит понять, и потому вычисляться будет по иной формуле, чем в классической физике. Да и называться он будет «релятивистским эффектом Доплера». Но СУТЬ его останется той же, и РЕЗУЛЬТАТ будет достаточно схожим:
_________________________________________________________
Эффект Доплера приводит к тому, что наблюдатель, движущийся относительно всех окружающих тел и материальных объектов со скоростью, близкой к скорости света, будет видеть все что происходит впереди него смещенным в фиолетовую область спектра и, главное, происходящим в неестественно быстром темпе, как будто он смотрит ускоренное кино, а все, что остается сзади по ходу его движения, он будет видеть смещенным в инфракрасную область света, и очень статичным, почти неподвижным.
_________________________________________________________
Это и есть ответ на первый принципиальный вопрос, поставленный в начале этой главы. Я привожу его здесь, еще до объяснения СТО, только потому, что практически такой же вывод следует и из классического, «до-релятивистского» эффекта Доплера, если не вдаваться в численную, формульную разницу, которая становится существенной только для околосветовых скоростей.
Сделаю еще одно, может быть, очевидное, но важное замечание: эффект Доплера существует только при условии, что скорость сигнала конечна. Если предположить, что сигнал передается мгновенно, эффект Доплера немедленно исчезнет! Так что, обнаружение светового эффекта Доплера послужило в своё время подтверждением конечности скорости света. Но об этом мы поговорим чуть позже.
В литературе по СТО приходится иногда встречать утверждение, что наличие эффекта Доплера служит одним из основных доказательств теории Относительности. Подобное утверждение является, по меньшей мере, грубой неточностью, ибо эффект Доплера, как мы только что видели, известен и объясним в рамках классической физики. На самом деле, доказательством СТО является наблюдаемое отклонение частоты сигнала от значения, определяемого классическим эффектом Доплера (кроме этого, доказательством может служить так называемый «поперечный» эффект Доплера – уменьшение частоты в направлении, перпендикулярном движению источника сигнала). Я допускаю, что на основании этого отклонения можно получить основные формулы СТО, но такой путь построения теории относительности кажется мне запутанным и неестественным. Поэтому оставим пока в стороне этот эффект — в конце концов, он еще послужит нам, как важный факт, подтверждающий справедливость СТО и совпадающий с ее выводами. Но мы не будем использовать его, как уже было сказано в начале главы, для вывода и обоснования главных принципов теории относительности.
Источник
В чем заключается эффект Доплера?
Эффект Доплера или доплеровский сдвиг возникает при движении наблюдателя относительно источника излучения (или наоборот) и заключается в изменении длины волны или частоты сигнала. Это явление, обнаруженное австрийским физиком Кристианом Доплером в 1803 году, может проявляться по-разному. Классическим примером данного эффекта является слышимое изменение высоты звука от проезжающей мимо машины скорой помощи. Программное обеспечение COMSOL Multiphysics® позволяет эффективно моделировать эффект Доплера в акустических системах и приложениях.
Первоначальная версия статьи была написана Александрой Фоули (Alexandra Foley) и опубликована 15 июля 2013 года. По сравнению с оригиналом данная заметка была значительно переработана, в неё были добавлены новые материалы и анимации на основе обновлённой версии демонстрационной модели, созданной в нашем пакете.
Суть эффекта Доплера
Мы часто сталкиваемся с эффектом Доплера, улавливая изменение высоты тона звука вследствие движения источника звука относительно неподвижного наблюдателя или, наоборот, при движении приемника относительно неподвижного излучателя. Когда источник звука неподвижен, звук, который мы слышим (будучи также в неподвижном состоянии), имеет ту же высоту (частоту), что и звук, непосредственно излучаемый источником.
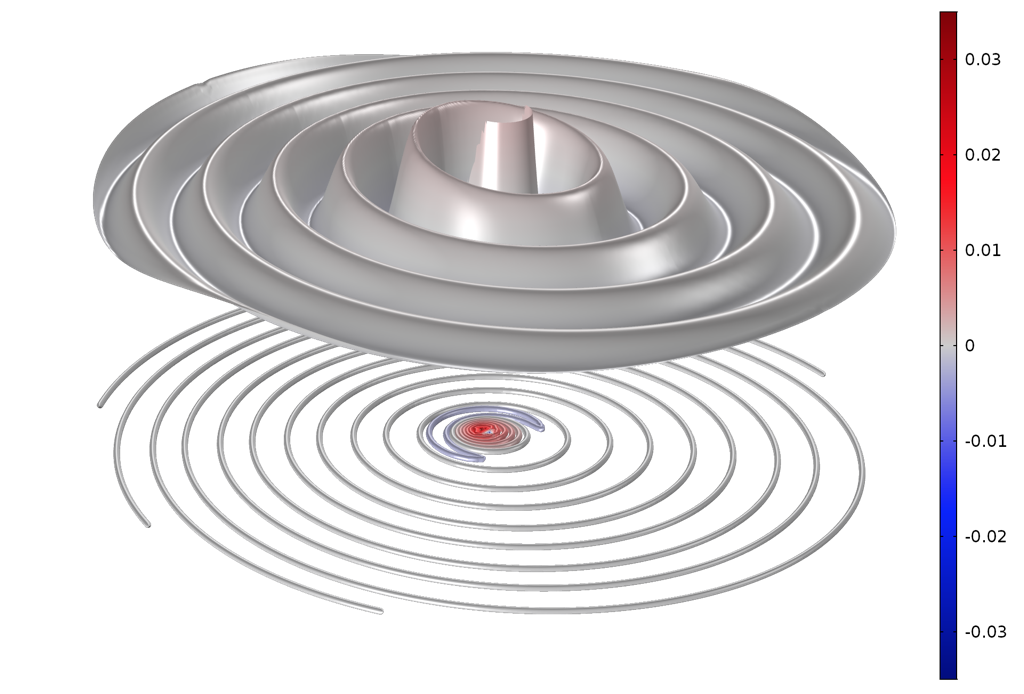
Звуковые волны, распространяющиеся от неподвижного источника звука в однородном потоке флюида. Данная постановка аналогична случаю, когда источник движется с постоянной скоростью.
При движении источника, звук, который мы слышим, изменяется. Вернёмся к примеру с машиной скорой помощи. Когда она проезжает мимо, сирена звучит иначе, чем если бы мы стояли непосредственно рядом с ней все время. Высота звука, создаваемого сиреной машины скорой помощи, изменяется, когда она приближается, проезжает прямо мимо нас и уезжает.
В процессе приближения машины каждая последующая звуковая волна излучается с более близкого расстояния, чем предыдущая. Из-за этого изменения положения для каждой последующей волны уменьшается время, за которое она доходит до нас. Следовательно, уменьшается расстояние между гребнями волны (длина волны), а значит частота волны увеличивается и звук воспринимается, как более высокий.
Это работает и в противоположном направлении. Когда источник звука удаляется, волны идут до нас всё дольше и дольше. Длина волны увеличивается, воспринимаемая частота уменьшается, высота звука понижается. Аналогичный эффект будет наблюдаться, если мы сами будет проезжать мимо припаркованной машины скорой помощи. В этом случае наблюдатель, то есть мы, движется к источнику. Каждая последующая звуковая волна всё быстрей доходит до нас по мере приближения.
Визуализация ещё одного примера эффекта Доплера
Другим наглядным примером эффекта Доплера является распространение волн на поверхности водоема. К примеру, жук лежит на поверхности лужи. Когда жук неподвижен, он все равно двигает конечностями, чтобы оставаться на плаву. Эти возмущения флюида распространяются по направлению от жука на поверхности воды в виде сферических волн.
Если жук начинает плыть, то это влияет на поток воды вокруг него. Пики волн следуют ближе друг к другу, когда жук приближается к нам и, наоборот, дальше, когда он уплывает. На анимации выше концептуально показано распространение волн на воде со скоростью, которая намного медленнее, чем скорость звука. Из-за маленькой скорости эффект Доплера в данном случае можно увидеть невооружённым глазом.
Численное моделирование эффекта Доплера
С использованием программного обеспечения COMSOL Multiphysics® и уникальных возможностей модуля расширения Акустика можно смоделировать эффект Доплера и рассчитать изменение частоты для источника, движущегося с заданной скоростью. Предположим, что воздух вокруг источника звука (в данном случае – это скорая помощь) движется со скоростью V = 50 м/с в отрицательном направлении по оси z. Также будем считать, что наблюдатель стоит на расстоянии 1 метра от скорой помощи, когда она проезжает мимо. На изображении ниже показан график зависимости звукового давления от расстояния для двух противоположных случаев, когда машина приближается и отдаляется от наблюдателя.

На этом графике по оси x представлено расстояние от машины скорой помощи до наблюдателя. Сплошной линией обозначен график звукового давления, которое воспринимает наблюдатель при приближении машины, а пунктирной линией — давление при удалении машины.
Представленный график позволяет увидеть, как амплитуда волны (или давление) быстрее уменьшается при удалении машины скорой помощи от наблюдателя по сравнению с тем, когда она приближается. Изменение амплитуды волны подтверждает наш эмпирический опыт: сирена становится тише по мере удаления от нас машины скорой помощи. Скорость, с которой уровень звука уменьшается при удалении скорой помощи, намного выше, чем скорость, с которой звук становится выше при приближении машины (как показано на графике выше).
Давайте теперь взглянем на этот эффект в немного другом представлении. Мы можем визуализировать уровень звукового давления вокруг источника звука. Помните, что источник движется в положительном направлении по оси z.
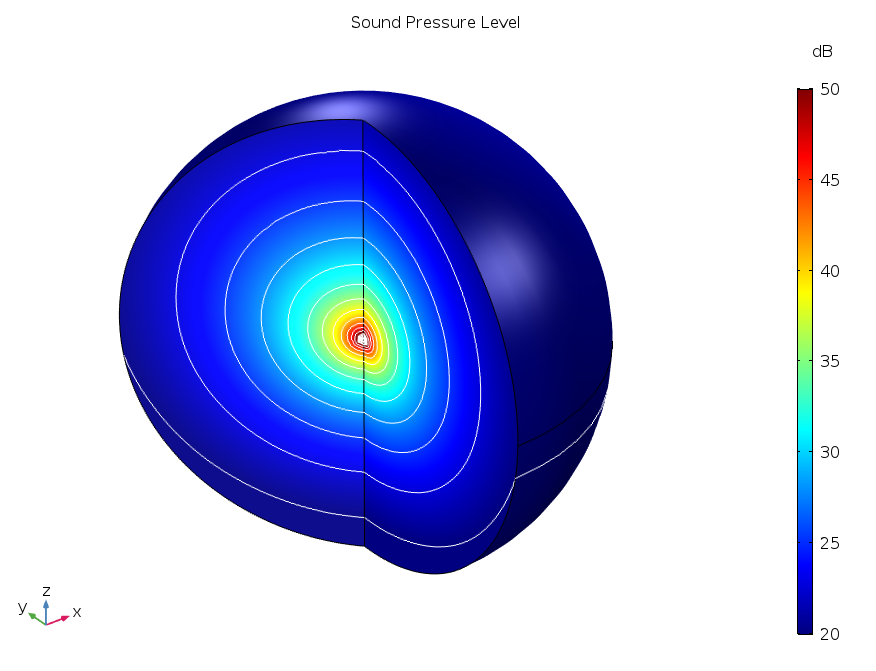
Распределение уровня звукового давления вокруг источника звука градиентом цвета и контурными линиями. Отчетливо видно, что самый внешний контур проходит через внутреннюю часть области моделирования к внешнему слою с идеально согласованными слоями (PML), область которые не показан на графике. Указанный факт также подтверждает тот факт, что звук ниже источника больше, чем над ним.
Другие примеры эффекта Доплера
Эффект Доплера проявляется (и используется) в самых различных приложениях. Одним из распространённых примеров является доплеровский радар, волновой пучок которого направляется на движущийся объект. Зная время, в течении которого волновой пакет доходит до цели, отражается и возвращается обратно к передатчику, можно рассчитать скорость цели. Доплеровский радар используется полицейскими для обнаружения машин, которые движутся быстрее, чем установленное скоростное ограничение.
Эффект Доплера также используется в астрономии для определения направления и скорости, с которой звёзды, планеты и галактики движутся относительно Земли. Измеряя изменение «цвета» электромагнитных волн, астроном может определить радиальную скорость небесного тела. В данном случае обычно оперируют терминами redshift или blueshift, т.е. красное или синее смещение. Если вы заметите «красную» звезду, это значит, что она довольно далеко от Земли. Кроме того, это явный индикатор того, что Вселенная расширяется!
Эффект Доплера также используется в метеорологических прогнозах, гидролокаторах, медицинской интроскопии, измерении кровотока и спутниковой связи.
Дальнейшие шаги
Нажмите на кнопку ниже, чтобы самостоятельно попробовать смоделировать эффект Доплера. При наличии учетной записи COMSOL Access и действующей лицензии на программное обеспечение вы сможете загрузить MPH-файл учебной модели, описанной в данной заметке.
Источник
