Как рассчитать эффективный заряд атома

Как рассчитать эффективный заряд ядра — Наука — 2021

Эффективный заряд ядра относится к заряду, ощущаемому внешними (валентными) электронами многоэлектронного атома после учета количества экранирующих электронов, окружающих ядро. Формула для расчета эффективного заряда ядра для одного электрона имеет вид «Zeff = Z — S», где Zeff — эффективный заряд ядра, Z — число протонов в ядре, а S — среднее количество электронной плотности между ядро и электрон, для которого вы решаете.

В качестве примера, вы можете использовать эту формулу, чтобы найти эффективный заряд ядра для электрона в литии, в частности, электрона «2s».

TL; DR (слишком долго; не читал)

Расчет эффективного заряда ядра: Zeff = Z — S. Zeff — эффективный заряд, Z — атомный номер, а S — величина заряда из правил Слейтера.

Найти Z: атомный номер

Определите значение Z. Z — число протонов в ядре атома, которое определяет положительный заряд ядра. Число протонов в ядре атома также известно как атомный номер, который можно найти в периодической таблице элементов.

В этом примере значение Z для лития равно 3.

Найти S: Правила Слейтера

Найдите значение S, используя правила Слейтера, которые предоставляют числовые значения для концепции эффективного заряда ядра. Это может быть достигнуто путем записи электронной конфигурации элемента в следующем порядке и группировках: (1s) (2s, 2p) (3s, 3p) (3d) (4s, 4p) (4d), (4f), ( 5s, 5p), (5d), (5f) и т. Д. Числа в этой конфигурации соответствуют уровню оболочки электронов в атоме (насколько далеко электроны от ядра), а буквы соответствуют заданной форме орбиты электрона. Проще говоря, «s» представляет собой сферическую орбитальную форму, «p» напоминает фигуру 8 с двумя лепестками, «d» напоминает фигуру 8 с пончиком вокруг центра, а «f» напоминает две фигуры 8, которые разделяют друг друга,

В этом примере у лития есть три электрона, и электронная конфигурация выглядит следующим образом: (1s) 2, (2s) 1, что означает, что на первом уровне оболочки находятся два электрона, оба со сферическими орбитальными формами, и один электрон (фокус этот пример) на втором уровне оболочки, также со сферической формой.

Найти S: назначить электронные значения

Назначьте значение электронам в соответствии с их уровнем оболочки и формой орбиты. Электроны на орбите «s» или «p» в той же оболочке, что и электрон, для которого вы решаете, дают 0, 35, электроны на орбите «s» или «p» в оболочке на один энергетический уровень ниже, дают 0, 85, а электроны на орбите «s» или «p» в оболочках два энергетических уровня и нижний дают вклад 1. Электроны на орбите «d» или «f» в той же оболочке, что и электрон, для которого вы рассчитываете, дают 0, 35, а электроны в орбита «d» или «f» на всех более низких энергетических уровнях вносит вклад 1. Электроны в оболочках выше, чем электрон, для которого вы решаете, не способствуют экранированию.

В этом примере в оболочке есть два электрона, которые на один энергетический уровень ниже, чем оболочка электрона, для которого вы решаете, и у них обоих есть «s» орбитали. Согласно правилам Слейтера, каждый из этих двух электронов вносит 0, 85. Не включайте значение для электрона, для которого вы решаете.

Найти S: добавить значения вместе

Рассчитайте значение S, сложив числа, которые вы присвоили каждому электрону, используя правила Слейтера.

В нашем примере S равно 0, 85 + 0, 85 или 1, 7 (сумма значений двух электронов, которые мы считаем)

Вычтите S из Z

Вычтите S из Z, чтобы найти эффективный заряд ядра, Зефф.

В примере с использованием атома лития Z равно 3 (атомный номер лития), а S равно 1, 7. Изменяя переменные в формуле на правильные значения для примера, он становится Zeff = 3 — 1.7. Значение Zeff (и, следовательно, эффективный заряд ядра 2s-электрона в атоме лития) составляет 1, 3.

Как рассчитать заряд иона

Чтобы рассчитать заряд иона, вычитая число или электроны из числа протонов в атоме.

Как рассчитать формальный заряд cocl2

При определении формального заряда молекулы, такой как CoCl2 (газ фосген), необходимо знать число валентных электронов для каждого атома и структуру молекулы Льюиса.

Источник

Как рассчитать эффективный заряд атома

ЭФФЕКТИВНЫЙ ЗАРЯД АТОМА, характеризует разность между числом электронов, принадлежащих данному атому в химический соединение, и числом электронов свободный атома. Для оценок ЭФФЕКТИВНЫЙ ЗАРЯД АТОМА з. а. используют модели, в которых экспериментально определяемые величины представляют как функции точечных неполяризуемых зарядов, локализованных на атомах; например, дипольный момент двухатомной молекулы рассматривают как произведение ЭФФЕКТИВНЫЙ ЗАРЯД АТОМА з. а. на межатомное расстояние. В рамках подобных моделей ЭФФЕКТИВНЫЙ ЗАРЯД АТОМА з. а. можно рассчитать, используя данные оптический или рентгеновской спектроскопии, ЯМР и др. Однако, поскольку электронная плотность в химический соединение делокализована и границ между атомами не существует, нельзя описать различные характеристики соединение одним набором Э. з. а.; значения этого показателя, определенные разными эксперим. методами, могут не совпадать. ЭФФЕКТИВНЫЙ ЗАРЯД АТОМА з. а. можно определить также на основе квантовохимический расчетов.
ЭФФЕКТИВНЫЙ ЗАРЯД АТОМА з. а., определенные в рамках к.-л. одной модели или в однотипных расчетах, используют для корреляции с различными физических-химический характеристиками соединение, установления реакционное центров в молекулах, оценки степени ионности химической связи.

Литература: Баринский Р. Л., Нефедов В. И., Рентгеноспектральное определение заряда атомов в молекулах, М., 1966.

Химическая энциклопедия. Том 5 >> К списку статей

Источник

1.2.3. Кристаллоструктурный метод расчета ионности связей и эффективных зарядов атомов в минералах

Этот метод базируется на двух основных постулатах: Химическая связь, осуществляемая связывающими межостовными электронами, рассматривается как взаимодействие ближнего порядка (ковалентного типа), оно происходит на расстояниях, отвечающих сумме ковалентных радиусов атомов. Иными словами, предполагается, что перераспределение электронной плотности в соединении между атомами происходит в пределах их первых координационных сфер, определяемых координационными числами (КЧ) атомов. В химических соединениях имеет место тенденция реализации электронейтрального состояния атомов. В рамках остовно-электронного подхода это означает стремление остовов к присоединению связывающих электронов с целью реализации состояния нейтральных атомов, поскольку процесс рекомбинации электронов экзотермичен. Другое дело, что разные остовы, обладая неодинаковыми силовыми характеристиками, в различной степени способны реализовать эту тенденцию, благодаря чему и получается то или иное распределение эффективных зарядов атомов в соединениях. Конкретная процедура оценки ионности (эффективных зарядов атомов) минералов производится в ряд этапов (Зуев, 1990):

1. Находится общее число валентных электронов минерала, равное суммарному заряду остовов с обратным знаком. Проблема оценки числа участвующих в химической связи электронов у атомов в соединениях подробно рассмотрена в предыдущем разделе 1.2.2.
2. Суммарное число валентных электронов минерала распределяется по соответствующим двухцентровым (межостовным) связям, т. е. оцениваются их электронные заряды.
3. Электронные заряды связей делятся на доли электронного облака, локализованные у атомных остовов пропорционально их силовым характеристикам.
4. Суммированием зарядов остовов и относящихся к ним долям электронных облаков вычисляются эффективные заряды атомов (ионов).

Как показано в монографии (Зуев, 1990), первый этап соответствует составлению остовно-электронной формулы (ОЭФ) соединения (минерала), второй — построению остовно-электронной модели (ОЭМ) соответствующей кристаллической структуры минерала, третий и четвертый этапы отвечают непосредственной оценке ионности связей и эффективных зарядов атомов с использованием кристаллохимических параметров соответствующей ОЭМ минерала. В качестве примеров приведем некоторые ОЭФ минералов и молекул, в которых по сравнению с монографиями (Зуев, 1990; Зуев, Денисов, Мочалов и др., 2000) внесены (в отдельных случаях) некоторые изменения (уточнения) в отношении фактической валентности неметаллов:

железо (α-Fe)

—

В этих формулах в квадратных скобках заключены атомные остовы, между которыми в круглых скобках находятся связывающие электроны (электриды). Неподеленные электроны показаны слева от катионного и справа от анионного остовов. Стрелки означают смещение связывающих электронов (электридов) к более электроотрицательному остову неметалла, указывая на полярный характер межатомных связей, а отсутствие стрелок под электридами указывает на ковалентный характер связей. Справа за прямой скобкой остовно-электронной формулы последовательно указаны координационные числа остовов и электридов, для последних имеет место линейное окружение остовами (КЧ = 2). Насколько правомерно или, другими словами, отвечает реальности представление кристаллов в виде ассоциации атомных остовов и связующих (а также неподеленных) электронов-электридов, что отражают предлагаемые остовно-электронные формулы? Подробное обоснование этого подхода имеется в уже достаточно обширной литературе (Bent, 1970; Гиллеспи, 1975; Cohen, 1984; Зуев, 1990; Гиллеспи, Харгиттаи, 1992; Семенов, 2001). Поэтому ограничимся лишь некоторыми дополнительными аргументами. Обычно ковалентную двухэлектронную связь трактуют в виде спаривания электронов у нейтральных атомов: например, Н-Н или Н ¯ Н ­ в простейшем случае молекулы водорода Н₂. Однако эти схемы явно упрощают реальную картину ковалентной связи, природу которой раскрывают квантово-химические методы (молекулярных орбит, валентных связей), в рамках которых необходимо учитывать обмен электронами у вступающих в связь атомов. Так, по Полингу (Полинг, 1974, с.140) молекулу водорода можно записать в виде резонанса двух структур: H_A ↓ H_B ↑­ и H_A ­↑ H_B ↓ Это значит, что электрон с положительным спином (↓) и электрон с отрицательным спином (­↑) меняются местами, т. е. происходит обмен электронами у атомов водорода.Понятно, что обмен электронами у первоначально нейтральных атомов водорода Н_А и Н_В предполагает отрыв у них электронов (с затратами энергий ионизации Ry = 13,6 эВ), образование остовов [H_A + ] и [H_B + ] и локализацию в межостовном пространстве ставшей общей (связующей) пары неразличимых электронов, которые попадают под действие силовых полей обоих остовов. Описанную ситуацию как раз и отражает остовно-электронная модель молекулы водорода — |[H + ](2e — )[H + ]|.[1] Аналогичным образом можно обосновать и другие более сложные остовно-электронные модели молекул и кристаллов. Имеются специальные формулы для оценки q в кристаллах (Зуев, 1990). Так, в случае простых (бинарного состава МхХу) минералов:

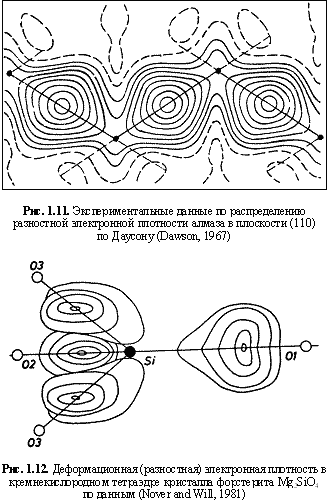
а в случае сложных минералов электронный заряд связи металл-неметалл находится по формуле:

(1.26)

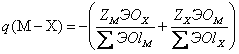
где Z_M, Z_X — числа валентных электронов атома, соответствующих зарядам остовов; ΣЭОl_M, ΣЭОl_X — суммы электроотрицательностей лигандов вокруг атомов М и Х в соответствующих атомных полиэдрах кристаллической структуры. Необходимые для таких расчетов координационные ЭО атомов имеются в (Зуев, 1990). Как показано ранее в разделе 1.2.1, исходя из сферической формы остовов и связывающих электронных облаков (электридов), обладающих соответствующими размерами и зарядами (рис. 1.3), можно строить остовно-электронные модели структур минералов. На рис. 1.4-1.8 даны примеры таких моделей для рутила, алмаза, кварца, сфалерита и периклаза. Важно подчеркнуть, что эти модели фактически демонстрируют новый остовно-электронный способ изображения кристаллических структур, в какой-то мере адекватный картам разностной электронной плотности (рис. 1.11-1.12), а также расчетам зарядовой электронной плотности в кристаллах по методу псевдопотенциала (Cohen, 1984). В последнем случае на соответствующих схемах, например, для кристалла Si, непосредственно фигурируют как связывающие электронные облака, так и остовы кремния. Остовно-электронные модели структур можно представлять в двух используемых в кристаллохимии аспектах (Зуев, 1990):

• как постройки из сферических остовов и электридов, обладающих соответствующими зарядами и радиусами (рис. 1.4-1.8);
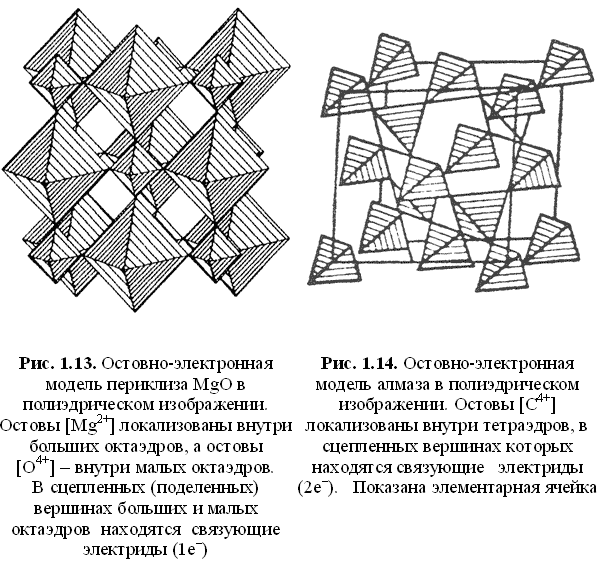
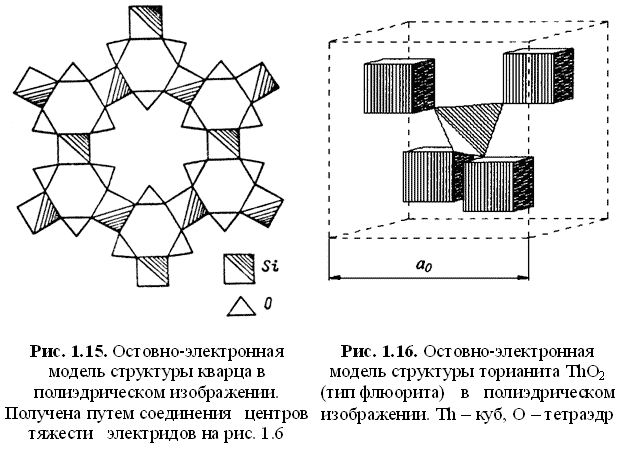
• как ассоциации остовных координационных полиэдров (рис. 1.13-1.16).

Во втором случае остовы катионных и анионных компонентов располагаются в центре соответствующих полиэдров, а связующие электроны локализованы в общих (поделенных) вершинах полиэдров. В свободных вершинах остовных полиэдров располагаются неподеленные электроны.

Полиэдрический способ изображения остовно-электронных моделей удобен и информативен: кристалл строится из сцепленных вершинами элементарных атомных (катионных и анионных) полиэдров-кирпичиков — октаэдров в структуре галита и периклаза, тетраэдров в структуре алмаза и сфалерита, кубов тория (церия) и тетраэдров кислорода в структуре торианита и церианита, октаэдров магния и тетраэдров кремния и кислорода в структуре форстерита и т. д. Согласно полиэдрическому способу изображения структуры, расстояние от центра полиэдра до общих (поделенных) вершин равно (по определению) ковалентному радиусу атома. Найденные по формулам (1.25) и (1.26) электронные заряды связей q(M-X) делятся между остовами пропорционально силовым параметрам F_M и F_X, в качестве которых можно использовать величины:

где L— общая лигандность остова, т. е. его координация с учетом неподеленных электронов. В монографии (Зуев, 1990) приведены многочисленные расчеты Q атомов в минералах с использованием параметров Z и соответственно F. Однако понятно, что одинаковые параметры Z слабо отражают индивидуальные химические особенности таких разных катионных остовов, как [Mg2+] и [Fe2+]. Поэтому более корректно, по-видимому, в формулах (1.27) вместо номинального заряда Z использовать суммарный эффективный заряд ядра, действующий на валентные (сверх остова) электроны атома — ΣZ_i*. Тогда эти формулы пре-образуются в:

где Z_i* — действующий на валентный электрон эффективный заряд ядра, вычисляемый по правилам С. С. Бацанова (Бацанов и Звягина, 1966; Бацанов, 1986), либо рассчитываемый из потенциалов ионизации атома по формуле (1.12). Именно второй способ оценки эффективных зарядов ядер, как более простой, принят в данной работе.

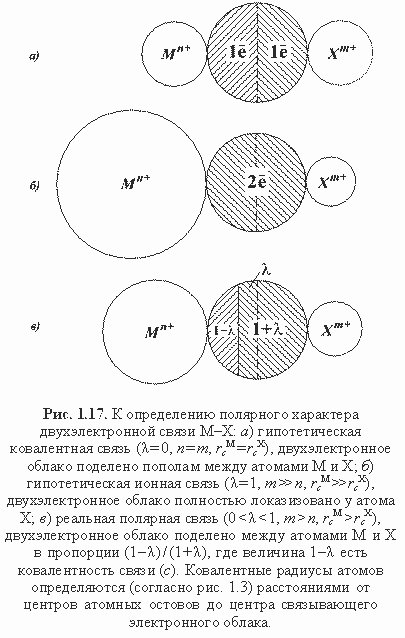
Использованием эффективных зарядов ядер в формулах (1.28) удается в явной форме, хотя и в суммарно усредненном виде, учесть силовые характеристики атома для всех его сверхостовных электронов. Так, в случае муассанита SiC, остовно-электронная формула которого |[Si 4+ ] (2e — )₄ [C 4+ ]|, совершенно очевидна необходимость учета эффективных зарядов ядер для всех четырех валентных электронов атомов Si и C при оценке их силовых параметров. Вычисленные по формулам (1.27) или (1.28) силовые параметры используются для расчета ионного (полярного) характера связей М-Х кристалла:

Многочисленные расчеты показали близость оценок ионности связей в минералах по обеим формулам, хотя вторая из них предпочтительнее. Схема полярной связи М-Х приведена на рис. 1.17, где чисто ионная связь (λ = 1) является лишь условной абстракцией. На самом деле прообразом такой связи является, например, неподеленная пара электронов при остове кислорода в кварце (рис. 1.6). В этом случае ввиду отсутствия второго (катионного) остова можно принять F_M = F_M* = 0, тогда по формулам (1.29) и (1.30) λ = 1, т. е. неподеленную пару при остове можно отождествить с химической двухэлектронной связью 100%-полярности. Поскольку в реальных связях М-Х с двумя остовами всегда F_M > 0 и F_M* > 0, то чисто ионные связи в гетероатомных химических соединениях (минералах) невозможны, соответственно нереальны предельно-ионные структуры типа Na + Cl — , Mg 2+ O 2- , Al₂ 3+ O₃ 2- и др. Впрочем, это не означает, что по распределению зарядов реальные кристаллические соединения не могут быть весьма близки к предельно-ионным моделям типа указанных, о чем свидетельствуют современные данные расчетов электронной плотности. Заключительная процедура вычисления эффективных зарядов атомов в минералах производится по следующим формулам (Зуев, 1990):

где N — порядок связи М-Х, равный q/2. Возможен расчет Q атомов в минералах на основе величин параметров q, минуя параметры λ. Обозначим через с — электронную долю связи, локализованную на катионном компоненте, а через q—c соответственно — на анионном компоненте связи М-Х. Тогда из пропорции с/(q—c) = F_M*/F_X*имеем:

Зная КЧ атомов М и Х в структуре минерала, приходим к следующим формулам:

которые дают те же самые результаты, что и формулы (1.31). Для сопоставления вычисленных по разработанной методике Q атомов в кристаллических соединениях с соответствующими данными их диэлектрической ионности по Филлипсу-Ван Фехтену рекомендуется выражение:

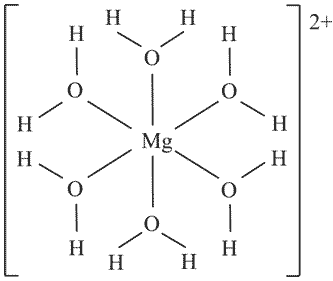
представляющее собой степень ионизации атомов, равную отношению эффективных зарядов к предельно-ионным зарядам атомов. В монографии (Зуев, 1990) даны примеры хорошего соответствия оценок эффективных зарядов атомов в кристаллах в рамках двух указанных подходов. Разработанная методика оценки ионности (эффективных зарядов атомов) универсальна в том смысле, что применима к соединениям различного типа, будь то молекулы, кристаллы, комплексы и т. д. Соответственно она была успешно апробирована на большом числе минералов и искусственных соединений. Для расчетов были использованы эффективные заряды ядер для валентных электронов атомов согласно (Zhang, 1982), электронные заряды связей в соединениях рассчитывались по приведенным формулам, либо непосредственно заимствовались из книги (Зуев, 1990). Ковалентные радиусы неметаллических компонентов r_c(X) были приняты с учетом данных Слэтера, Урусова, Лебедева (Лебедев, 1969; Урусов, 1975; Зуев, 1990), а металлических — находились по разности r_c(M) = d(M-X) — r_c(X), где d(M-X) — среднее межатомное расстояние катион-анион в структуре. В качестве примеров рассчитаем эффективные заряды атомов в молекуле NaCl, галите NaCl, cфалерите ZnS, периклазе MgO, кварце SiO₂, форстерите Mg₂SiO₄ и бишофите MgCl₂(H₂O)₆. Остовно-электронная формула молекулы NaCl — |[Na + ]2e — [(Cl 7+ )6e — ]|, она обладает ординарной полярной связью Na-Cl. Размерные характеристики молекулы: d(Na-Cl) = 2,36 Å, r_c(Cl) = 0,7 Å, r_c(Na) = 1,66 Å. Эффективные заряды ядер для остовов ΣZ_i*(Na + ) = 1,78, ΣZ_i*(Cl + ) = 2,82, по формулам (1.28) F*(Na + ) = 1,78/1,662 = 0,646, F*(Cl+) = 2,82/0,72 = 5,755, по формуле (1.30) l(Na-Cl) = (5,755 — 0,646)/(5,755 + 0,646) = 0,8, т. е. получаем Na+0.8Cl-0.8, что соответствует ионности, вычисленной из дипольного момента молекулы NaCl (Бацанов, 1986). Остовно-электронная формула галита была приведена выше, q(Na-Cl) = 1e-, d(Na-Cl) = 2,82 Å, r_c(Cl) = 1,0 Å, r_c(Na) = 1,82 Å, в этом случае F*(Na + ) = 1,78/(6×1,822) = 0,09, F*(Cl 5+ ) = 23,76/(6×12) = 3,96. По формуле (1.30) λ(Na-Cl) = 0,96 и далее по формулам (1.31): Q(Na) = 1 — 6×0,5(1 — 0,96) = +0,88, Q(Cl) = 5 — 6×0,5(1 + 0,96) = -0,88, т. е. для галита имеем Na +0.88 Cl -0.88 , что соответствует диэлектрической ионности кристалла NaCl (Бацанов, 1982). Обратим внимание на заметный рост эффективных зарядов атомов при переходе от молекулы к кристаллу. В сфалерите ZnS КЧ атомов равны 4, q(Zn-S) = 2e — , d(Zn-S) = 2,35 Å, F*(Zn 2+ ) = 6,83/(4×1,35 2 ) = 0,94, F*(S 6+ ) = 30,35/(4×1 2 ) = 7,59, по формуле (1.30) λ(Zn-S) = 0,78 и далее по формулам (1.31), в которых N = 1: Q(Zn) = 2 — 4(1 — 0,78) = +1,12 и Q(S) = 6 — 4(1 + 0,78) = -1,12, т. е. для сфалерита получаем Zn +1.12 S -1.12 . В периклазе MgO (рис. 1.8) КЧ обоих атомов равны 6, q(Mg-O) = 1e — , d(Mg-O) = 2,10 Å, r_c(O) = 0,55 Å, r_c(Mg) = 1,55 Å, SZ_i*(Mg 2+ ) = = 5,21, SZ_i*(O 4+ ) = 13,94, F*(Mg 2+ ) = 5,21/(6×1,55 2 ) = 0,361, F*(O 4+ ) = 13,94/(6×0,55 2 ) = 7,68. По формуле (1.30) находим λ(Мg-O) = 0,91 и далее по формулам (1.31) Q(Mg) = 2 — 6×0,5(1 — 0,91) = +1,73, Q(O) = 4 — 6×0,5(1 + 0,91) = -1,73. В итоге получаем для периклаза Mg +1.73 O -1.73 . В случае кварца SiO₂ (рис. 1.6) КЧ(Si) = 4(O), КЧ(О) = 2(Si), q(Si-O) = 3e-, d(Si-O) = 1,61 Å, r_c(O) = 0,55 Å, r_c(Si) = 1,06 Å, SZ_i*(Si 4+ ) = 15,205, SZ_i*(O 4+ ) = 13,94, F*(Si4+) = 15,205/(4×1,06 2 ) = 3,383, F*(O4+) = 13,94/(2×0,55 2 ) = 23,04. По формуле (1.30) λ(Si-O) = 0,744 и далее по формулам (1.31) находим: Q(Si) = 4 — 4×1,5(1 — — 0,744) = +2,46, Q(O) = 4 — 2×1,5(1 + 0,744) = -1,23. Таким образом, для кварца имеем Si +2.46 O₂ -1.23 , что соответствует его диэлектрической ионности f_i = 0,6 (Бацанов, 1982). В форстерите Mg₂SiO₄, структура которого характеризуется КЧ(Mg) = 6(O), КЧ(Si) = 4(O) и КЧ(О) = 3Mg+Si, усредненные электронные заряды связей, межатомные расстояния и ковалентные радиусы атомов: q(Mg-O) = 1,23e — , q(Si-O) = 2,31e — , d(Mg-O) = 2,12 Å, d(Si-O) = 1,63 Å, r_c(Mg) = 1,57 Å, r_c(Si) = 1,08 Å, r_c(O) = 0,55 Å. Суммарные эффективные заряды ядер для валентных электронов атомов — ΣZ_i*(Mg 2+ ) = 5,21, ΣZ_i*(Si 4+ ) = 15,205, ΣZ_i*(O 4+ ) = 13,94, силовые параметры остовов — F*(Mg 2+ ) = 5,21/(6×1,57 2 ) = 0,352, F*(Si 4+ ) = 15,205/(4×1,08 2 ) = 3,259, F*(O 4+ ) = 13,94/(4×0,55 2 ) = 11,521. По формуле (1.30) λ(Mg-O) = 0,941, λ(Si-O) = 0,559 и далее по формулам (1.31): Q(Mg) = 2 — 6×0,615(1 — 0,941) = +1,782, Q(Si) = 4 — 4×1,155(1 — 0,559) = +1,963, Q(O) = 4 — 3×0,615(1 + 0,941)-1×1,155(1 + 0,559) = -1,382, т. е. приходим к Mg₂ +1.78 Si +1.96 O₄ -1.38 . Найденные в форстерите эффективные заряды оказались удивительно близкими к полученным японскими учеными из прецизионных расчетов электронной плотности — Mg₂ +1.75 Si +2.1 O₄ (Fujino, Sasaki, Takeuchi, Sadanada, 1981). В качестве заключительных примеров расчета Q атомов рассмотрим комплексные кристаллические соединения. Бишофит, как показали структурные исследования, имеет молекулярную структуру, состоящую из октаэдрических комплексов [Mg(H₂O)₆] 2+ , нейтрализованных двумя ионами Cl — . Соответственно формула минерала — [Mg(H₂O)₆] 2+ Cl₂ — , а структурная формула отдельного иона [Mg(H₂O)₆] 2+ :

Здесь атом кислорода, имея плоско-треугольную координацию — КЧ(О) = Mg+2H, находится, по-видимому, в состоянии 3s2p 2 -гибри­дизации с неподеленной парой 2s 2 -электронов, и соответственно с остовом [O 4+ ]. Межатомные расстояния: d(Mg-O) = 2,08 Å, d(H-O) = 1,0 Å, ковалентные радиусы: r_c(Mg) = 1,53 Å, r_c(H) = 0,43 Å, r_c(O) = 0,55 Å. Исходное распределение заряда в комплексе — [Mg2+(H₂O)₆], т. е. число валентных электронов у атома магния равно нулю. Тогда расчет по формуле (1.26) дает q(Mg-O) = -[(0x3,5)/(6×3,5) + (4×1,3)/(1,3 + 2×2,1)] = 0,945e — , q(H-O) = -[(1×3,5)/(1×3,5) + (4×2,1)/(1,3 + 2×2,1)] = 2,527e — . Силовые параметры остовов: F*(Mg 2+ ) = 5,21/(6×1,53 2 ) = 0,37, F*(H + ) = 0,85/(1×0,43 2 ) = 4,6, F*(O 4+ ) = 13,94/(3×0,55 2 ) = 15,36. Воспользовавшись в данном случае формулами (1.32), для связи Mg-O находим с = 0,0224e — , q—c = 0,9231e — , а для связи H-O c = 0,5824e — , q—c = 1,9446e — . Далее по формулам (1.33) находим Q(Mg) = 2 — 6×0,0224 = +1,866, Q(H) = 1 — 1×0,5824 = +0,417, Q(O) = 4 — 1×0,9231 — 2×1,9446 = -0,812. Результирующее распределение зарядов атомов в бишофите оказалось следующим — [Mg +1.866 x(H₂ +0.417 O -0.812 )₆] 2+ Cl₂ — . Баланс зарядов в молекуле воды приводит к (H₂O) +0.022 , что позволяет понять природу примеси ковалентной составляющей связи в данном и других аква-комплексах.[2] Как это очевидно, дело заключается в незначительной перекачке электронной плотности от молекул воды на свободные орбитали центрального катиона. Результатом этого является некоторое уменьшение формального заряда центрального катиона и соответственно — появление на молекулах воды указанного избыточного положительного заряда. Другими словами, от каждой из шести первоначально электронейтральных молекул воды на свободные орбитали центрального катиона (Mg 2+ ) переходит 0,022e-, и он приобретает эффективный заряд +2 — 0,022×6 = +1,868. В случае бианкита ZnSO₄x6H₂O конституцию этого минерала можно рассматривать как соединение из октаэдрических и тетраэдрических комплексных ионов — [Zn(H₂O)₆] 2+ и [SO₄] 2- . Расчет приводит к следующим эффективным зарядам атомов в октаэдрическом комплексе [Zn +1.83 (H₂ +0.418 O -0.807 )₆] 2+ . Эффективные заряды атомов в комплексе [SO₄] 2- вычислены для структуры с двойными связями и следующими параметрами: d(S-O) = 1,50 Å, r_c(O) = 0,5 Å, r_c(S) = 1,0 Å, q(S-O) = 4,0e — , F*(S 6+ ) = 30,35/(4×1 2 ) = 7,59, F*(O 2+ ) = 5,19/(1×0,52) = 20,76. Использование этих параметров приводит к следующим эффективным зарядам в сульфатном комплексе– [S +1.72 O₄ -0.93 ] 2- , а общее распределение зарядов в бианките будет таковым: [Zn +1.83 (H₂ +0.418 xO -0.807 )₆] 2+ [S +1.72 O₄ -0.93 ] 2- . Для водного сульфата FeSO₄×6H₂O аналогичные расчеты приводят к следующему распределению эффективных зарядов — [Fe +1.86 (H₂ +0.411 O -0.80 )₆] 2+ [S +1.72 O₄ -0.93 ] 2- . Для октаэдрического аква-комплекса Fe(III) расчеты дали такие эффективные заряды атомов — [Fe +2.69 (H₂ +0.424 O -0.796 )₆] 3+ . Для безводных сульфатов M(II)SO₄, структура которых характеризуется следующей взаимной координацией атомов: КЧ(М) = 2О_А + 4О_В, КЧ(S) = 2O_A + 2O_B, КЧ(О_А) = M + S, КЧ(О_В) = 2М + S, получились в порядке уменьшения Q(M) такие данные:

Mn +1.843 [S +1.418 O_2(A) -0.662 O_2(B) -1.969 ] Mg +1.837 [S +1.577 O_2(A) -0.70 O_2(B) -1.01 ] Fe +1.812 [ S +1.50 O_2(A) -0.677 O_2(B) -0.979 ] Cu +1.812 [S +1.577 O_2(A) -0.696 O_2(B) -0.998 ] Co +1.806 [ S +1.577 O_2(A) -0.695 O_2(B) -0.996 ] Zn +1.793 [S +1.577 O_2(A) -0.693 O_2(B) -0.991 ] Ni +1.788 [S +1.577 O_2(A) -0.692 O_2(B) -0.99 ]

Обратим внимание на антибатный ход изменения эффективных зарядов нерадикальных катионов M(II) и радикальных катионов S(VI) в рассмотренном ряду сульфатов и некоторое уменьшение Q(S) при переходе от свободного радикала [SO₄] -2 к связанному в кристаллической решетке безводному сульфату. В таблице 1.32 приведены результаты оценок эффективных зарядов в ряде комплексов и молекул с плоско-треугольной и тетраэдрической координацией центрального атома кислородными лигандами. Таблица 1.32 Эффективные заряды атомов в некоторых комплексах и молекулах, рассчитанные в предположении двойных связей «катион-кислород»

Комплекс (молекула)	d(M-On),Å	Эффективныезаряды атомов	Комплекс	d(M-O4),Å	Эффективные заряды атомов
[NO3] —	1,24	N +0,58 O3 — 0.527	[ClO4] —	1,51	Cl +1.81 O4 — 0.703
[CO3 ] 2 —	1,28	C +1 O3 — 1	[MnO4] —	1,59	Mn +2.22 O4 — 0.805
[SO4 ] 2 —	1,50	S +1.72 O4 — 0.93	[CrO4 ] 2 —	1,65	Cr +2.53 O4 — 1.133
ArO4	1,50	Ar +1.94 O4 — 0.485	[WO4 ] 2 —	1,80	W +2.8 O4 — 1.2
FeO4	1,50	Fe +2 O4 — 0.5	[MoO4 ] 2 —	1,83	Mo +3.06 O4 — 1.26

В рамках продемонстрированного подхода были выполнены расчеты Qатомов в тех же минералах, что и в монографии (Зуев, 1990, стр. 55, таблица 3.9), в результате выяснилась близость расчетных эффективных зарядов атомов в обоих случаях и подтвердились три общих закономерности распределения этих зарядов в сложных минералах: 1) явление (или эффект) взаимного влияния катионов (ВВК); 2) различие в эффективных зарядах кристаллохимически нетождественных (по числу или сорту координирующих катионов) анионов, например, кислорода, обозначаемых О_А, О_В, О_Си т. д.; 3) выполнения известного второго правила Л. Полинга о локальной компенсации ионных зарядов в структуре, если в качестве таковых использовать рассчитанные величины Q атомов. Эффект ВВК проиллюстрируем следующими уравнениями с указанием эффективных зарядов атомов:

Mg +1.73 O -1.73 +Si +2.46 O₂ -1.23 = Mg +1.79 Si +2.20 O₃ ;

2Mg +1.73 O -1.73 +Si+2.46O₂ -1.23 = Mg₂ +1.78 Si +1.96 O₄ -1.38 ;

Zr +3.21 O₂ +Si +2.46 O₂ -1.23 = Zr +3.36 Si +2.14 O₄ -1.375 ,

т. е. в сложном минерале (энстатите, форстерите, кианите, цирконе) по сравнению с простыми составляющими оксидами (периклазом, кварцем, корундом, бадделеитом,) происходит увеличение Q (уменьшение ковалентности связи) более слабого катиона (Mg, Al, Zr) за счет уменьшения Q (роста ковалентности связи) более сильного катиона (Si). Подробно эффекты ВВК в сложных минералах рассмотрены в монографии (Зуев, 1990), однако по поводу эффектов ВВК необходимо сделать весьма существенное дополнение, упущенное в указанной монографии. В самом деле, как меняется ионность (ковалентность) связей при переходе от исходных простых составляющих к сложному минералу? Для выяснения данного вопроса сравним средние параметры ионности f_i и ковалентности (f_c = 1-f_i) для простых составляющих кристаллов, с одной стороны, и для соответствующего сложного соединения, с другой стороны. Такие сравнительные оценки удобно произвести по анионным компонентам соединений с использованием формулы 1.34, примеры соответствующих оценок приведены в таблице 1.33. По данным последнего (пятого) столбца таблицы 1.33 четко выявляется не имеющая исключений закономерность понижения ионности и роста ковалентности в сложном кристалле относительно этого параметра (естественно, среднего) в соответствующих простых составляющих кристаллах. Расчеты показали, что аналогичная картина имеет место и в случае содержащих более двух сортов катионов сложных кристаллических соединений, например: Ca₃Al₂Si₃O₁₂ (Δf_i/Df_c = -0,07/+0,07), Mg₃Al₂Si₃O₁₂ (Δf_i/Df_c = -0,04/+0,04), CaTiSiO₅ (Δf_i/Δf_c = -0,05/+0,05), Be₃Al₂Si₆O₁₈ (Δf_i/Δf_c = -0,02/+0,02) и т. д. Таблица 1.33 Характер изменения параметров ионности и ковалентности в сложных кристаллических соединениях по сравнению с простыми составляющими кристаллами

Mg +1.7 3 O — 1. 73 , Si +2.46 O₂ — 1.23

Mg +1.79 Si +2.2 O₃ — 1.33

2Mg +1.73 O — 1.73 , Si +2.46 O₂ — 1.23

Источник

Q атомов в простых кристаллах	fi/fc	Q атомов в сложном кристалле	fi/fc	Dfi/Dfc