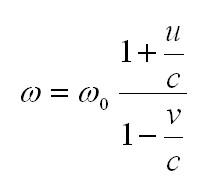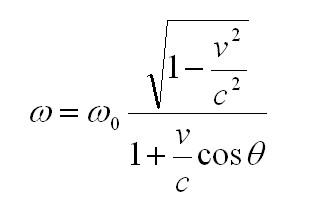Основы радиолокации
Эффект Допплера
Рисунок 1. К пояснению эффекта Допплера
Рисунок 1. К пояснению эффекта Допплера
Эффект Допплера
В радиолокации эффект Допплера используется при решении следующих задач:
- измерение скорости лоцируемого объекта;
- селекция движущихся целей (СДЦ); (MTI — Moving Target Indication;)
- в бортовых авиационных или космических радиолокационных системах — для точного определения наклонных дальностей.
Эффект Допплера (применительно к акустическим волнам) — это заметное изменение частоты или высоты тона звукового колебания, возникающее когда источник звука движется по направлению к слушателю или от него. Этот эффект, открытый австрийским физиком Кристианом Допплером (Christian Doppler) , применим к волновым процессам различного происхождения.
Упомянутое заметное изменение частоты между излучаемой и принимаемой волнами происходит из-за относительного движения источника и приемника волны. Для понимания эффекта Допплера предположим вначале, что частота звукового колебания источника поддерживается постоянной. Длина волны такого колебания также будет постоянной. Если источник звука и приемник остаются неподвижными, то приемник будет «слышать» звук с той же частотой, что излучается источником. Это связано с тем, что приемник принимает такое же количество волн (периодов колебания) в единицу времени, что и количество волн, издаваемых источником колебания.
Если же теперь представить, что либо источник перемещается по направлению к приемнику, либо приемник перемещается в сторону источника, либо оба они движутся навстречу друг другу, то приемник будет принимать звук более высокой частоты нежели звук, который издается источником. Теперь приемник будет принимать большее количество волн (периодов колебания) в единицу времени и, следовательно, интерпретировать принятую волну как колебание более высокой частоты. В обратной ситуации, когда источник колебания и приемник расходятся друг от друга, приемник будет принимать меньшее количество волн (периодов колебания) в единицу времени и, значит, воспринимать их как колебание меньшей частоты. При этом и в первом, и во втором случаях источник колебания издает звук на одной и той же постоянной частоте.
Например, звуковой сигнал быстро движущегося автомобиля (Рисунок 1) слышится более высоким при его приближении, чем когда автомобиль удалаяется. В данном случае звуковой сигнал автомобиля издает акустические колебания на одной и той же частоте и рапространяются они в воздухе с одинаковой скоростью во всех направлениях, а расстояние между автомобилем и слушателем уменьшается. В результате этого, каждый новый период звукового колебания проходит меньшее расстояние до точки приема, чем предыдущий. Таким образом, периоды колебания приходят с уменьшающимися временными интервалами между ними.
| fD = | 2·v | fD частота Допплера [Гц] λ = длина волны [м] v = скорость движения источника колебания [м/с] |
| λ |
Данное выражение будет корректным, если в качестве множителя v (скорости источника) будет подставлена его радиальная скорость. Однако самолет может лететь в направлении, отличающемся от направления на радиолокатор. В этом случае частота Допплера будет определяться только радиальной составляющей полного вектора скорости самолета. Поскольку в общем случае эти два вектора не совпадают, формула для частоты Допплера примет вид:
| fD = | 2·v | · cos α | fD частота Допплера [Гц] λ = длина волны [м] v = скорость движения источника колебания [м/с] α = угол между направлением линии визирования цели (направлением линии между антенной и целью) и направлением полета цели. |
| λ |
Вывод формулы для частоты Допплера
Набег фазы φ , который приобретает электромагнитная волна при распространении от антенны радиолокатора до цели и обратно (Рисунок 2), равен отношению длины пройденного волной пути к длине излучаемой волны, помноженному на градусную меру полного цикла колебания ( 2·π ):
Рисунок 2. Набег фазы принятого сигнала
Рисунок 2. Набег фазы принятого сигнала
| φ = − | 2r · 2π | φ = разность фаз между излученным и принятым сигналом; 2r = — удвоенное расстояние до цели (туда и обратно); 2π = 360°: фазовый набег за один период колебания; λ = длина волны излучаемого сигнала. |
| λ |
Данное выражение справедливо, если цель неподвижна. В этом случае разность фаз между излученным и принятым сигналом будет постоянной. Если же цель имеет некоторую радиальную скорость.
| vr = | d(r) |
| dt |
то значение разности фаз будет изменяться. Продифференцировав выражение для разности фаз по времени, получим
| d(φ) | = | — 4π · vr |
| dt | λ |
Как известно, производная фазы колебания по времени есть его частота. Поэтому из приведенных выше выражений может быть получена формула для частоты Допплера — частотного сдвига, который приобретает сигнал, ортазившийся от двигающегося объекта:
| fD = | 1 | · | d(φ) | = | 1 | · | — 4π · vr |
| 2π | dt | 2π | λ |
| | fD| = | 2 · vr | = | 2 · vr· ftx | where: | ftx = is the transmitters frequency c0 = is the speed of the light vr = is the radial speed of the aim |
| λ | c 0 |
Полученная формула позволяет сделать вывод о том, что в практике радиолокации эффект Допплера возникает дважды: первый раз — на пути зондирующего сигнала от радиолокатора к цели, второй — на пути отраженного от цели (и уже имеющего допплеровский сдвиг частоты) сигнала в обратном направлении.
Нормированная частота Допплера
Частота Допплера зависит от двух переменных: радиальной скорости цели и несущей частоты передатчика радиолокатора. Если частота передатчика постоянна, то частота Допплера является мерой только радиальной скорости цели. Современные радиолокаторы, в основном, представляют собой радиолокаторы с частотным разносом. Частота излучения таких радиолокаторов не является постоянной. В данном случае влияние различия частот излучения все еще остается незначительным. Однако если частоты излучения находятся в разных частотных диапазонах, то обычная обработка радиолокационных сигналов не является возможной. При цифровой обработке радиолокационных сигналов допплеровская частота будет делиться на текущую частоту излучения для исключения влияния разницы между частотами излучения.
Теперь допплеровская частота является мерой только радиальной скорости цели и называется «нормированной». Принятые эхо-сигналы при зондировании на различных частотах теперь могут обрабатываться обычным путем.
Издатель: Кристиан Вольф, Автор: Андрій Музиченко
Текст доступен на условиях лицензий: GNU Free Documentation License
а также Creative Commons Attribution-Share Alike 3.0 Unported License,
могут применяться дополнительные условия.
(Онлайн с ноября 1998 года)
Источник
Эффект Доплера для чайников: суть явления, применение, формула
Эффект Доплера – важнейшее явление в физике волн. Прежде чем перейти напрямую к сути вопроса, немного вводной теории.
Колебание – в той или иной степени повторяющийся процесс изменения состояния системы около положения равновесия. Волна — это колебание, которое способно удаляться от места своего возникновения, распространяясь в среде. Волны характеризуются амплитудой, длиной и частотой. Звук, который мы слышим — это волна, т.е. механические колебания частиц воздуха, распространяющиеся от источника звука.
Вооружившись сведениями о волнах, перейдем к эффекту Доплера. А если хотите узнать больше о колебаниях, волнах и резонансе — добро пожаловать в отдельную статью нашего блога.
Суть эффекта Доплера
Самый популярный и простой пример, объясняющий суть эффекта Доплера – неподвижный наблюдатель и машина с сиреной. Допустим, вы стоите на остановке. К вам по улице движется карета скорой помощи со включенной сиреной. Частота звука, которую вы будете слышать по мере приближения машины, не одинакова.
Сначала звук будет более высокой частоты, когда машина поравняется с остановкой. Вы услышите истинную частоту звука сирены, а по мере удаления частота звука будет понижаться. Это и есть эффект Доплера.
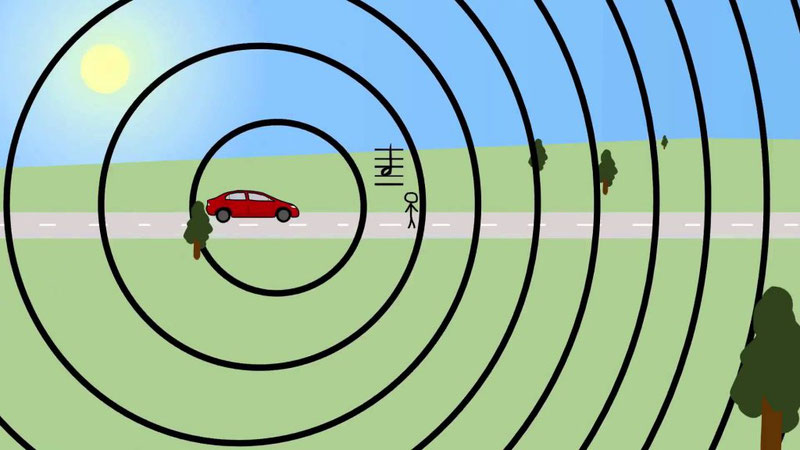
Частота и длина волны излучения, воспринимаемого наблюдателем, изменяется вследствие движения источника излучения.
Если у Кэпа спросят, кто открыл эффект Доплера, он не задумываясь ответит, что это сделал Доплер. И будет прав. Данное явление, теоретически обоснованное в 1842 году австрийским физиком Кристианом Доплером, было впоследствии названо его именем. Сам Доплер вывел свою теорию, наблюдая за кругами на воде и предположив, что наблюдения можно обобщить для всех волн. Экспериментально подтвердить эффект Доплера для звука и света удалось позднее.
Выше мы рассмотрели пример Эффект Доплера для звуковых волн. Однако эффект Доплера справедлив не только для звука. Различают:
- Акустический эффект Доплера;
- Оптический эффект Доплера;
- Эффект Доплера для электромагнитных волн;
- Релятивистский эффект Доплера.
Именно эксперименты со звуковыми волнами помогли дать первое экспериментальное подтверждение этому эффекту.
Экспериментальное подтверждение эффекта Доплера
Подтверждением правильности рассуждений Кристиана Доплера связано с одним из интересных и необычных физических экспериментов. В 1845 году метеоролог из Голландии Христиан Баллот взял мощный локомотив и оркестр, состоящий из музыкантов с абсолютным слухом. Часть музыкантов – это были трубачи – ехали на открытой площадке поезда и постоянно тянули одну и ту же ноту. Допустим, это была ля второй октавы.
Другие музыканты находились на станции и слушали, что играют их коллеги. Абсолютный слух всех участников эксперимента сводил вероятность ошибки к минимуму. Эксперимент длился два дня, все устали, было сожжено много угля, но результаты того стоили. Оказалось, что высота звука действительно зависит от относительной скорости источника или наблюдателя (слушателя).

Применение эффекта Доплера
Одно из наиболее широко известных применений – определение скорости движения объектов при помощи датчиков скорости. Радиосигналы, посылаемые радаром, отражаются от машин и возвращаются обратно. При этом, смещение частоты, с которой сигналы возвращаются, имеет непосредственную связь со скоростью машины. Сопоставляя скорость и изменение частоты, можно вычислять скорость.
Эффект Доплера широко применяется в медицине. На нем основано действие приборов ультразвуковой диагностики. Существует отдельная методика в УЗИ, называемая доплерографией.
Эффект Доплера также используют в оптике, акустике, радиоэлектронике, астрономии, радиолокации.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Открытие эффекта Доплера сыграло важную роль в ходе становления современной физики. Одно из подтверждений теории Большого взрыва основывается на этом эффекте. Как связаны эффект Доплера и Большой взрыв? Согласно теории Большого взрыва, Вселенная расширяется.
При наблюдении удаленных галактик наблюдается красное смещение – сдвиг спектральных линий в красную сторону спектра. Объясняя красное смещение при помощи эффекта Доплера, можно сделать вывод, согласующийся с теорией: галактики удаляются друг от друга, Вселенная расширяется.
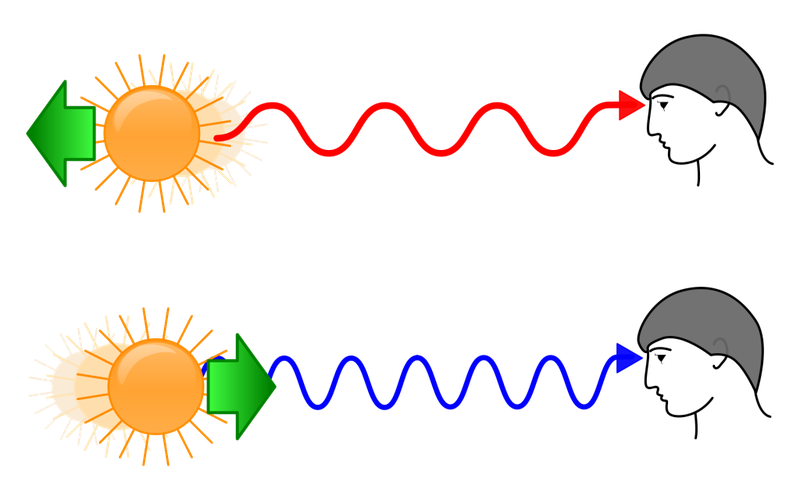
Формула для эффекта Доплера
Когда теорию эффекта Доплера подвергали критике, одним из аргументов оппонентов ученого был факт, что теория помещалась всего на восьми листах, а вывод формулы эффекта Доплера не содержал громоздких математических выкладок. На наш взгляд, это только плюс!
Пусть u – скорость приемника относительно среды, v – скорость источника волн относительно среды, с — скорость распространения волн в среде, w0 — частота волн источника. Тогда формула эффекта Доплера в самом общем случае будет выглядеть так:
Здесь w – частота, которую будет фиксировать приемник.
Релятивистский эффект Доплера
В отличие от классического эффекта Доплера при распространении электромагнитных волн в вакууме для расчета эффекта Доплера следует применять СТО и учитывать релятивистское замедление времени. Пусть света – с, v – скорость источника относительно приемника, тета – угол между направлением на источник и вектором скорости, связанным с системой отсчета приемника. Тогда формула для релятивистского эффекта Доплера будет иметь вид:
Сегодня мы рассказали о важнейшем эффекте нашего мира – эффекте Доплера. Хотите научиться решать задачи на эффект Доплера быстро и легко? Спросите у специалистов студенческого сервиса, и они охотно поделятся своим опытом! А в конце — еще немного про теорию Большого взрыва и эффект Доплера.
Источник